λx:Math.Metal

appendix

Contents

Rust

Rust: C++ + ML

functional: ADTs, recursion (map, fitler, fold), parametric polymorphism (generics)

borrow checker: affine types, ownership types

Programming Languages

Page 13 of Lisp 1.5 manual

Programming languages have a dual nature to them. On one hand, logicians treat them as mathematical objects whose semantics (a function from programs to values) are amenable to formalization. e.g. SML, Scheme, WASM. On the other, engineers treat them as tools for their trade whose purpose is to build applications; eg: Python, Javascript, and Ruby.

In this document we will be covering the foundations of programming languages both:

  1. inductively by implementing an interpreter for CMU's teaching language C0 and comparing it to the common semantic core that all languages share.
  2. deductively (in the near future) by formalizing the semantics which the interpreter implements, similar to C0deine

Starting the study of the principles of programming languages with definitional interpreters is convenient as it allows us to operationalize a common core of semantics without worrying about the semantic chasm that lies between syntax and the electrons. todo: need to contrast to mathematical . dual nature. we will start with def. interpreters. Rather than use the chip's implementation with microcode as the interprter, we will build our own interpreter in software. In the development of our C0 interpreter, we won't smoke test it with too many programs, since 1. the focus here is on principles of programming languages and 2. there is close to no real usage of C0 outside CMU. In the next document, we will add the complexity of the semantic chasm back in by implementing a compiler for C89, targeting RV32I.

The data an interpreter (and compiler) uses to represent a program is abstract syntax, in contrast to the concrete syntax — this distinction was introduced in Landin's infamous paper: Next 700 Programming Languages. Parsing maps this concrete syntax to abstract syntax, and evaluating maps the abstract syntax to a value. If you take a step back, a parser and evaluator are adjoint functors to one another, just like probability and statistics. A parser is a function that maps information to data (abstract syntax), and an evaluator is a function that maps data back to information. Coloquially, a parser lifts the representation and the evaluator lowers it. Most of the time, the abstract syntax is represented with a tree.

Keep in mind that the code below provides sketches, and is not functional as is. This is similar to how one might sketch out a proof to provide intuitions before proceeding with the full formalization. If you'd like to take a look at the full implementation, take a look at picoc089. It's quite hackable (and should be even more so after reading this document).

We will implement a fully functional programming language with a single int type.

  • Arnold 2010
  • Pfenning 2021

    • Contents

    Parsing

    Academia formalizes frontend parsing from concrete to abstract syntax via lexical, syntactic and semantic analysis. The result are well-defined compiler compilers that take in a series of symbols from an alphabet as input and produce a series of productions from a grammar.

    Contents

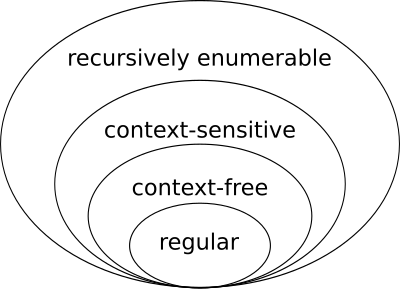
    Compiler parsing has a strong connection computational theory and linguistics. There's a fancy-schmancy-chomsky hierarchy that models the different levels of expressitivity in grammars. Languages which RE/FA are too weak to recognize (for instance, unbounded balanced parenthesis), motivate the jump to BNF/PA. These foundations can be useful for theoreticians (pump it, louder!) and perhaps language designers, but there's nothing practical with respect to compiler construction for existing languages.

    Lexing

    Lexical analysis:
- alphabet (input): characters
- grammar (output): tokens (regular language)
    - spec: regular expressions (RE)
    - impl: deterministic finite automata (DFA)

    Grammar:

    // introductions
LITERAL_INT      ::= [0-9]+
ALIAS            ::= [a−zA−Z][a−zA−Z0−9]*

// eliminations
PLUS             ::= +
MINUS            ::= -
STAR             ::= *
SLASH            ::= /

// keywords
KEYWORD_INT      ::= int
KEYWORD_INT      ::= main
KEYWORD_VOID     ::= void
STMT_RETURN      ::= return
STMT_IF          ::= if
STMT_WHILE       ::= while

// punctuation
PUNC_LEFTPAREN   ::= (
PUNC_RIGHTPARE   ::= )
PUNC_LEFTBRACE   ::= {
PUNC_RIGHTBRAC   ::= }
PUNC_SEMICOLON   ::= ;
        

    #[rustfmt::skip]
#[derive(Clone, PartialEq, Serialize, Deserialize, Debug)]
pub struct Token { pub lexeme: String, pub typ: TT }

#[rustfmt::skip]
#[derive(Copy, Clone, PartialEq, Serialize, Deserialize, Debug)]
pub enum TT {
    LiteralInt, Alias, // introductions (values) RE: [0-9]+ and [a-zA-Z][a-zA-Z0-9]*
    KeywordInt, KeywordChar, KeywordVoid, KeywordRet, KeywordIf, KeywordEls, KeywordFor, // keywords ⊂ identifiers
    Plus, Minus, Star, Slash, LeftAngleBracket, RightAngleBracket, Equals, Bang, Amp, Bar, // eliminations (ops)
    PuncLeftParen, PuncRightParen, PuncLeftBrace, PuncRightBrace, PuncSemiColon, // punctuation
}

    This is the

    Parsing

    Syntactic analysis:
- alphabet (input): tokens
- grammar (output): tree (context-free)
    - spec: Backus-Naur Form (BNF)
    - impl: pushdown automata (PA)

    Grammar:

    <prg>    ::= <func>
<func>   ::= KEYWORD_INT KEYWORD_MAIN PUNC_LEFTPAREN KEYWORD_VOID
             PUNC_RIGHTPAREN PUNC_LEFTBRACE <statement> PUNC_RIGHTBRACE

<stmt>   ::= KEYWORD_RETURN <expr> PUNC_SEMICOLON
<expr>   ::= LITERAL_INT
           | <expr> <binop> <expr>

<binop>  ::= PLUS
           | MINUS
           | STAR
           | SLASH

<val> ::= literalint

    The syntactic grammar specified above via BNF is a subset of the C language. It only recognizes and parses programs that return arithmetic expressions. The <program> production refers to <function>, which, in turn, refers to <statement>, but these can be easily rewritten as one single RE. The one rule which REs cannot specify is the <exp> production; it refers to itself an arbitary amount of times.

    Top down: recursive descent

    calling it top down but starting with the terminals w weakest binding power makes sense under the assumption that you are traversing the tree with a post-order

    Grammar notation Code representation Terminal Code to match and consume a token Nonterminal Call to that rule’s function | if or switch statement * or + while or for loop ? if statement

    Recursive descent parsers is the resulting implementation when the code follows the data. They descend top-down the grammar's spec predictively — produces a unique production with a single character lookahead LL(1) — rather than employ backtracking.

    When you’re writing a parser, recursive descent is as easy as spreading peanut butter. It excels when you can figure out what to parse based on the next bit of code you’re looking at. That’s usually true at the declaration and statement levels of a language’s grammar since most syntax there starts with keywords—class, if, for, while, etc.

    Parsing gets trickier when you get to expressions. When it comes to infix operators like +, postfix ones like ++, and even mixfix expressions like ?:, it can be hard to tell what kind of expression you’re parsing until you’re halfway through it. You can do this with recursive descent, but it’s a chore. You have to write separate functions for each level of precedence (JavaScript has 17 of them, for example), manually handle associativity, and smear your grammar across a bunch of parsing code until it’s hard to see.

    Top down w/ operator precedecne: pratt

    Typing

    Semantic analysis
- alphabet (input): tree
- grammar (output): attributed tree (context-sensitive)
    - spec: ??
    - impl: ??
    References

    Evaluation

    Let us begin with the code for an interpreter which can evaluate arithmetic (a glorified calculator, really).

    Arithmetic

    
#[derive(Debug, Clone)]
pub enum Expr {
    Num(i32),
    Add {
        l: Box<Expr>,
        r: Box<Expr>,
    }
    Mult {
        l: Box<Expr>,
        r: Box<Expr>,
    },
}

fn eval(e: &Expr) -> Num {
    match e {
        Expr::Num(n) => n,
        Expr::Add { l, r } => eval(*l) + eval(*r),
        Expr::Mult { l, r } => eval(*l) * eval(*r),
    }
}

mod tests {
    use super::*;

    #[test]
    fn test() {
        assert_eq!(9, eval(Expr::Num(9)));
        assert_eq!(19, eval(Expr::Add{
            l: Expr::Num(9),
            r: Expr::Num(10),
        }));
    }
}

    Intuitively, the language defined here is expressive enough such that all other arithmetic can be reduced (desugared) down to its Add and Mult constituents; subtraction is addition with negative numbers, and division is multiplication with fractions. todo: c0 just uses the host semantics of rust's i32. if you don't want to inherit from your host semantics (and for compiler, the chip's semantics of IEEE754, you can do something like racket's numbers which is mini mathematica).

    Bindings, Functions

    Whether a variable is still "alive" "active" "visible", is formally asked, as whether or not the variable is still *bound* in the current *scope*.

    (let1 (x 9) (let1 (x 10)) (+ x x)) we want this to produce 20. we just set 10, why would we want it to be 9? (let1 (x 9) (+ x (let1 (x 10)) (+ x x))) we just agreed the rhs is 20 the previous case we want the lhs to be 9 total is 29 (let1 (x 9) (+ (let1 (x 10)) (+ x x) x ) ) spatial locality: a variable's binding is determiend by the position in the source program (ast), not by the order of the program's execution. 29 reasonable (static scope spatial locality). same idea as fp rather than oop. 30 not reasonable # lisp, python, javascript dynamic scope (temporal locality) let is making the semantics much clearer, since we're *creating* a binding, NOT *updating* e.g. (let1 (x 9) (+ (if false 4 (let1 (x 10)) (+ x x)) // false could be if the moon is full... x ) ) - syntax, static types, dynamic types, doesn't matter.

    where something is bound, is purely a matter of the program syntax. we always walk up the tree.

    guy steele said lisp's dynamic scope does NOT make sense. see master's thesis. fixed it up, made scheme. mcarthy said he was inspired by something in lambda calculus, but then realized their mistake and made common lisp. python made same mistake. javascript made the same mistake.

    interp(subst: number/Exprc * symbol * Expr -> ExprC)

    funcApplication: find the function, pull out it's body substitute in the body, get a new expr back. (that expr may have other functions left).

    formal parameter with the actual parameter

    MOST PROFOUND FUNDAMENTAL THEOREM (exploring more in nov?) subst: number vs Exprc. call by value vs call by expr (f (+ 5 4))

    SMOL makes the exec decision: call by value (eager). rather than lazy. show in code. it's either we eval the expr and then extend the nv with the variable bounded value, or extend the nv with variable bounded to the expr, and then eval come elimination time (via nv lookup)

    (let1 (x 9) (let1 ) ) local binding Exp ... (let1E (var: String)*(val:String)*(body:Exp)) functions

    at this point, SMoL has functions as values. C in contrast only has top level functions

    intro: f = lam(). elim: f()

    abstract syntax (represent with data) deffunc: (id String) * (formalparam String) * (body Expr) applyfunc: (lookup fnv (id String)) where fnv: Map

    decision decision: - lambda formal parameter is just onesf - lambda bodies only have a single Expr. not multiple.

    - SMOL: order: eval function first or eval applicatino first h(): (+ g(z) g(w)) // left or right? motivation for sequential vs parallel computation. def f(x): x + 9 def g(y): f(y + 10) g(11) interp: name: Symbol identifier: Symbol body: ExprC (needs to be stronger than ArithC with identifiers)

    scope (informally, inductively): a block (environment block--of bindings?) is a sequence of defs followed be a sequence of exprs. SMoL has a top level block, and function blocks. environment extends from the current environment.

    f(x): x+y y:=3 f(4) // OK, because y is defined in the environment (f's sub environment) at the time of evaluation y:=8 f(x): y:=3 x+y f(4)+y # y here uses top level env f(x): y:=3 x+y f(4)+y # ERROR, since after applying f(4), top level env still has no y bound (defined) x := 9 g(): x f(): x := 10 g() f() # produces 9, not 10. ?????????? WHAAA ????????? how do i square this and the first code example?? # i see. environment inheritance is static. not dynamic. it's at function definitoin. NOT applicaiton. x := 1 f(): x:=2 g() g(): x f() # produces 1, since g()'s environment at time of DEF is x=1 (env of top level) x := 1 f(): g(): x x:=2 g() f() # produces 2, since g()'s environment at time of DEF is x=2 (env of f)

    basically have to look at the current environment at the time of some function f's definition. you can't just "look up in the text to see the last line where x is defined." you have to look at the *environment* and hoist all the definitions on top. like we do here. emphasis is on environment, not lines of code.

    x:= 4 x:= 8 # error. why?? because the semantic concept of scope is *envs* think about it like this. f(x, x): x+x f(9,10) ## what should this produce?? this is why the code above should error.

    Control flow

    some langs are boolean strict (non-permissive). some are more permissive and have "truthy/falsy" values

    guido, brandon. none of their intuitions on truthy/falsy values agree.

    racket: truthy/falsy. gives one false value (false), everything else is truthy. shriram still perfers boolean strict. but if you must have flexibility, do it this way. easier to remember for user's when they load the table in their head

    Heap

    References

    Formal Semantics

    Constructive Logic

    Type Theory

    Present C0's static and dynamics in typed lambda calculus along with a progress/preservation proof.

    References